The Toughest SAT Geometry Problems Explained (by a Perfect 800 Math Scorer!)

By Laura Whitmore

If you've taken or prepared for the SAT, especially Module 2 (math section), you've probably felt that moment when a really tough geometry question pops up. Your heart might start racing, your stomach churns, and suddenly you're feeling overwhelmed. Trust me—this is completely normal. Geometry problems on the SAT can be notoriously tricky, but here's some good news: I'm about to break down three of the hardest geometry problems that show up repeatedly on the test!

Not in a reading mood? Watch our YouTube video instead!

---

Before We Dive In: A Quick Heads-Up on Practice Resources

All three problems I’ll walk through here are taken directly from page 282 of our newly updated SAT Math Workbook. This workbook—and all of our updated videos—will be available in our revamped self-paced math course launching this May. If you're already enrolled or planning to join soon, you'll get full access as soon as it's released!

---

👉 Tangent Lines and Right Triangles (Disguised Circle Problems)

A common scenario on the SAT is that problems appear to be about circles, but they're really testing you on triangles. For example, you'll often see questions involving tangent lines. Remember, "tangent" means the line touches the circle at exactly one point and forms a right angle with the radius.

Here's how a typical problem looks: You have a circle with a given radius, and lines tangent to the circle meet at a point outside the circle, forming a quadrilateral. Students often panic here, but here's the trick—just draw a radius from the center to the tangent points. You'll form two right triangles. From there, you can use congruent triangles and the Pythagorean theorem (a² + b² = c²) to find the missing lengths.

Key Takeaway: Tangent lines form right angles. When you see "tangent," immediately think "right triangle."

---

👉 Equilateral Triangles Inside Circles (Using Special Right Triangles)

Another tricky question is when you're given an equilateral triangle (a triangle with all three sides equal) inside a circle. You're usually given the perimeter or side lengths and asked to find the radius. Here's the common mistake students make: they'll incorrectly draw the radius from the center directly to the midpoint of one of the sides, creating an unknown gap. Don't do this! Instead, draw the radius directly to a vertex (corner). This ensures no gaps and creates a clear triangle.

Once you correctly draw the radius to the vertex, you'll see an isosceles triangle (two equal sides). Often, these become special 30-60-90 triangles. Remember:

• Opposite the 30° angle: side length x

• Opposite the 60° angle: side length x√3

• Hypotenuse (opposite the 90° angle): side length 2x

This strategy helps you quickly determine the radius.

Key Takeaway: Draw the radius to a vertex and look for special triangles (30-60-90) whenever you see a √3.

---

👉 Similar Triangles Hidden in Circle Problems

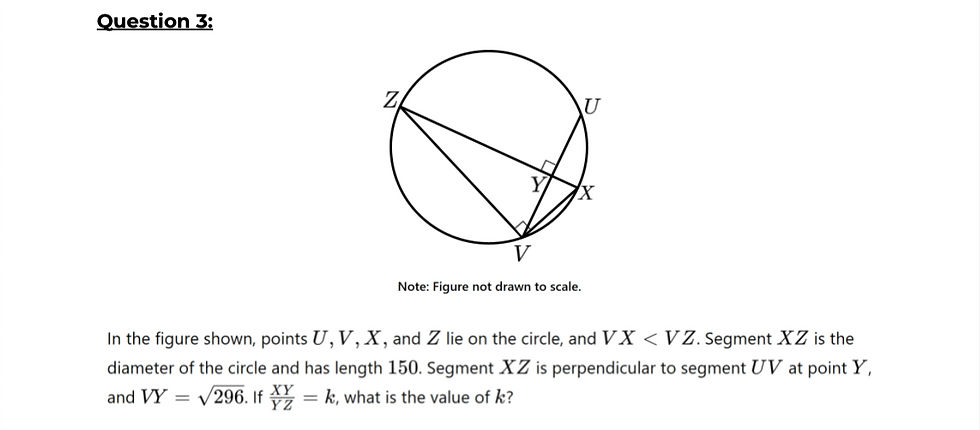
Sometimes SAT problems are complicated by showing circles combined with multiple right triangles. These questions aren't really about circles—they're testing your ability to recognize similar triangles and set up proportions.

You'll often see one big right triangle with smaller right triangles inside. The key is identifying shared sides between these triangles. By labeling unknown segments with variables (like x and 150 – x), you can easily set up proportions and cross-multiply to solve for unknown sides. Often, this process will lead you to a simple quadratic equation (ax² + bx + c = 0). Solve this using a calculator or tool like Desmos, and you'll quickly find the lengths you need.

Key Takeaway: Identify similar triangles, set up proportions clearly, and solve carefully. It's rarely about circles—it's about triangles and algebra.

---

Final Tips to Remember:

• If you feel stuck on a geometry question, it's okay to skip and return later. These are usually the most time-consuming questions.

• Always draw pictures clearly and carefully.

• Remember, geometry on the SAT frequently disguises triangles as circles. Stay alert for this trick.

Happy prepping!