By Laura Whitmore
Have you recently taken the SAT and felt overwhelmed by the math section? You’re not alone, and it’s a common experience for many. My tutor team and I want to share some valuable insights into five subtly tricky math problems that often trip up students on the SAT. Our goal is to help you feel more confident and prepared for your next test!
Want to skip the reading? Check out my YouTube video instead!
#1 Understanding the Sum of Solutions in Quadratic Equations
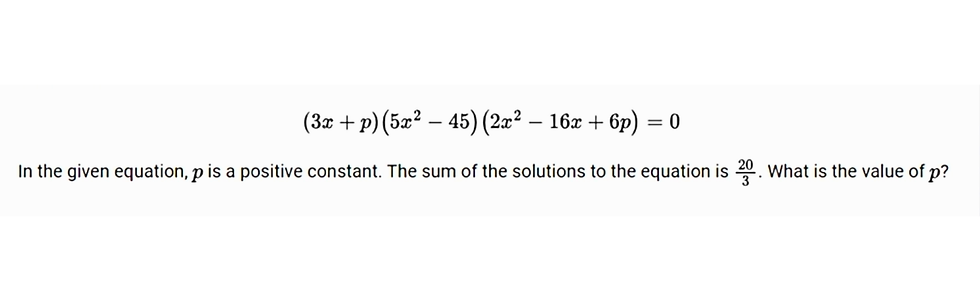
One common challenge is dealing with equations where you need to find the sum of solutions. This often appears more complicated than it actually is. A quick and effective strategy is to use the formula “-B/A” from the quadratic equation. For example, if you encounter a question where the sum of the solutions is given, applying this formula can simplify the problem significantly.
Quick Tip: Always keep this shortcut in mind for the test: the formula “-B/A” will save you time and reduce errors when working with quadratics.
#2 Tackling Equations with No Real Solutions
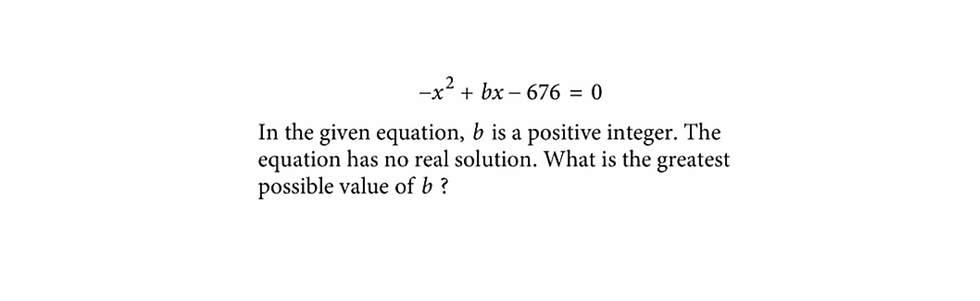
Another tricky type of problem involves recognizing when an equation has no real solutions. The key to identifying this is through the discriminant, which is the part of the quadratic formula under the square root: B² - 4AC. If the discriminant is less than zero, there are no real solutions. In practical terms, knowing this can help you quickly eliminate answer choices and zero in on the correct answer.
Remember: Practice identifying the discriminant in equations; it’s a valuable skill for boosting efficiency on test day.
#3 Converting Vertex Form to Standard Form
Some SAT math problems require converting a parabola’s vertex form into standard form to find values like A, B, and C. This is especially useful when dealing with questions that ask for the sum of these values. Make sure you’re comfortable with expanding and rearranging these forms—getting this right can often be the difference between a correct and incorrect answer.
Pro Tip: Memorize the different forms of quadratic equations: standard, factored, and vertex form. This foundational knowledge will simplify many of the harder questions you encounter.
#4 Solving Systems of Linear Equations
System of linear equation problems can be deceptively simple or surprisingly tricky. A quick way to handle them is by graphing the equations to find where the lines intersect. If you’re using a calculator, graph both equations and look for the intersection point—this visual approach is often the quickest path to the right answer.
Quick Tip: Practice graphing linear equations manually and with a calculator. Familiarity with both methods will ensure you can tackle these problems no matter the format.
#5 Translating Word Problems into Equations
Word problems that involve translating phrases like “70% less” or “80% greater” into equations can be challenging without the right approach. The key is to understand the language: “less” means subtract, and “greater” means add. So, for “70% less,” you’re looking at 30% of the original amount, which translates to 0.3B if B is your variable. Similarly, “80% greater” would translate to 1.8 times the variable.
Practical Advice: Practice breaking down word problems into step-by-step calculations. It’s all about finding the right translation of words into numbers.
These are just a few examples of the tricky math problems that often appear on the SAT. Mastering these types of questions can significantly boost your test scores and confidence.
If you’re looking for more in-depth strategies and practice, I highly recommend our Digital SAT Self-Paced Math Course—this course offers exclusive video lessons and walkthroughs of all the important concepts you need to know to succeed on the SAT Math section.
Happy prepping!
Comments